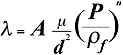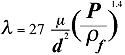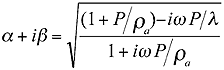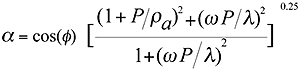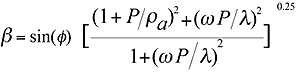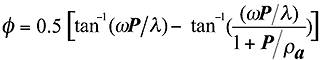Bradbury's Fiber Equations [1]

(editor's note: the moving fiber hypotesis has been pretty much discredited, so take this with a grain of salt)

To be able to define the effect of stuffing density on TL response, it is necessary to define the fiber's effect on attenuation and phase, thus the change of air velocity for the TL Terminus signal. The principal term in the fiber equations is the fiber drag parameter (l). This designation is unfortunate since it is also used to designate wavelength, however changing it would lead to confusion when referencing the Bradbury's paper where these equations are derived. If there is a mystery in the TL design it lies in the fibers drag parameter. The aerodynamic drag due to sound waves in a fiber mass where the fiber diameter is small, typically about 0.01 mm, is given by:

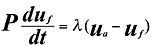
The left-hand side of equation is mass * acceleration and the right-hand is the aerodynamic drag. The relationship between the drag parameter l and packing density P is based on the theory of the flow past small cylinders and spheres and is expressed as:

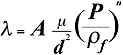Equation 1

There is some uncertainty in the definition of the constants A and n, but as tentative expression, it will be assumed that the drag parameter is given by:

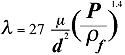Equation 2

m is the coefficient of viscosity of air, m = 1.81x10^-5kg/(m sec) at normal room temperature, d = is the fiber diameter, and P is the packing density of the fiber material, and rf is the density of the fiber material. Therefore P/rf is the proportion of the volume taken up by the fibers. As an example of fiber parameters, the following table shows the variation between Fiberglass and Long–Hair Wool, two of the principal fibers used in the TL line.

Table 1: Fiber Type Characterization   Fiberglass Long-Hair Wool Packing density, P 21 kg/m3 35 kg/m3 Measured fiber diameter, d 0.005 mm 0.028 mm Estimated flow resistance, l 12 600 N sec/m4 5700 N sec/m4

By specifying d and P quantities that characterize a specific fiber type, l the flow resistance can be calculated. With the flow resistance l defined, the fiber's attenuation and change of air velocity can be estimated. When the D c limit is known, the causes for the TL's non-linearity for lengths > 2 meters can be understood. This implies that by manipulating these two parameters a new type of fiber for stuffing density can be proposed and it's effectiveness studied, ie Miraflex or AcoustaStuff. The attenuation and change of velocity in a fiber mass is described by the following equation:

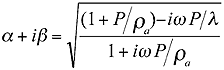Equation 3

where a is related to the velocity component and b the attenuation component. The behavior of Equation 3 for low and high frequencies can be deduced as, at low frequency

when , wP/l --> 0 we have 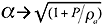and b --> 0

In other words, the speed of sound is reduced to

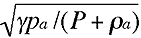
and there is no attenuation of the wave. This is consistent with the observed data for attenuation but leaves the change in speed of sound at best a non calculated quantity in that a phase shift, for example @ 20Hz vs @ 50Hz, is not defined. Unknown is the frequency at which the attenuation slope begins in an unstuffed line. At high frequencies, the limiting cases are more difficult to obtain, but it can be shown that as a -->0 and b --> 1/2l/raw the speed of sound approaches the ordinary adiabatic speed of sound, but the wave is attenuated at a rate of

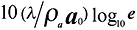
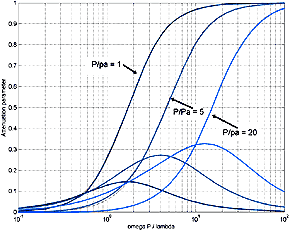
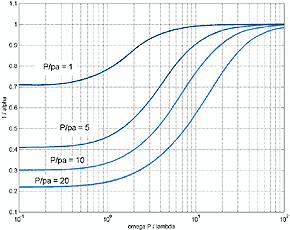
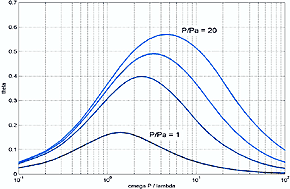
however this is hardly a useful quantitative definition. A quantitative view is realized by plotting the a and b components of equation 3.

Equation 4a Equation 4b where   Equation 4c

Solving Equations 4a and 4b for Wool fiber, P/ra ratios in the range of 1 to 20 generate the following plots.

Fig. 3.0 Attenuation vs. P/pa ratios Click Image for Larger Chart Fig. 3.1 Velocity vs. P/pa ratios Click Image for Larger Chart

The top curves are normalized as 2b (w P/l )/(P/ra), while the bottom curves are the b calculation. This clearly shows the frequency shift to higher values as Dtr is increased. A similar but scaled by Dtr value shift is seen in the Dtr=1 curve vs frequency. Note that Fig.3.1 graph for P/ra=1, ie unstuffed line indicates that the low frequencies will be phase shifted while the harmonics of the TL line will be attenuated asymptotically An inescapable conclusion of the data in Fig.3.2 is that for low frequencies and high fiber densities the air molecule interaction with the fibers approaches that of a viscous flow phenomena than that of an adiabatic or isothermal phenomena.

Fig. 3.2 Click Image for Larger Chart Equations 4a and 4b, contain a f term as sin(f) and cos(f) respectively. This causes a shift in the frequency and thus in the slope of Fig.3.1 and 3.2. The graphing of the arctan function helps to illustrate this effect.

Fig 4.0 Bradbury's Attenuation Data Click Image for Larger Chart Fig. 4.1 Bradbury's Change in Air Velocity Data Click Image for Larger Chart

Fig.4.0 and 4.1 are Bradburys measured data for fiberglass and wool vs computed data curves (I have left out the measured data points to clean up the plots). The data shows the difference in fiber characteristics but more importantly the projected response at low frequency ie < 50 Hz where Bradbury notes that the measured data and theoretical are in poor agreement. This is an important region since it defines the TL stuffing density non-linearity problem that is of concern for TL low frequency design. Fig. 4.0 is fairly straight forward and is only interesting in that it shows the greater effectiveness in harmonic attenuation for frequencies > 100Hz. Thus fiberglass can be used as a stuffing medium for TL line length < 0.9 m. Fig. 4.1 on the other hand is full of implications; for one it indirectly defines Dt for the TL line, and shows graphically the low frequency problem for lines > 1.5m or Fr < 50 Hz.

As mentioned previously, Bradbury's measured data stops at about 50 Hz thus Fig.4.2 is an extrapolation. The second qualification is that the P/ra ratios are quite high, for instance the TLB value for wool would be about 8-9 vs. the 17.5 used. However for the purpose of this analysis, this is not a serious impediment. Referencing Fig. 3.2 it is apparent that as P/ra decreases that the 1/a curves will move up and that for practical values of stuffing density the fiber flow resistance imposes a limit of the D speed of air in the fiber mass. Thus as a best case Fiberglass curve flattens out around 50Hz and wool shows a minimum 1/a ratio of 0.2 or ~ 130m/sec. This implies that an effective barrier to the necessary phase change via stuffing density exist. As an example the TLB has a Dtr=8.2 for wool and an estimated air velocity in the fiber mass of 129.8 m/sec,or an a ratio of 0.377 namely wool as an effective fiber is near it's limit for a TL line length = 1 m. This is supported by empirical data which shows that it is very difficult to achieve the necessary Terminus gain for a line > 1.5 m. Fig. 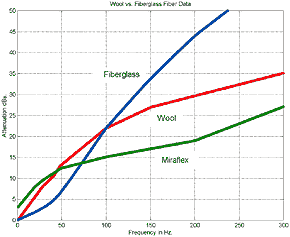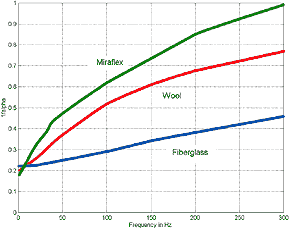4.2 Low Frequency Change of Speed Data Click Image for Larger Chart While data for Miraflex as fundamental fiber parameters is non existent, L. de Martin (2) has graciously provided some attenuation and change of speed data that he has taken in his own study. Emphasizing that it is very preliminary in nature, it gives an indication that it might be useful for TL lines in the 2-meter range.

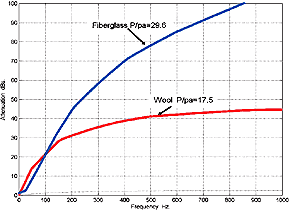
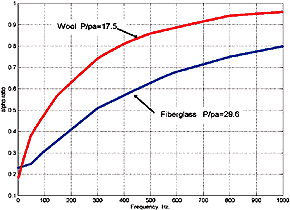
Fig.4.3 Low Frequency Miraflex Attenuation Data Click Image for Larger Chart Fig.4.4 Low Frequency Miraflex Change of Air Speed Data Click Image for Larger Chart

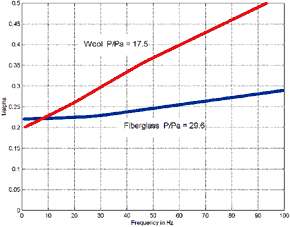
Note: that Dacron HoloFill fiber type would lie in between the fiberglass and wool plots and that given the relative values that can be correlated to the empirical data for stuffing density vs. line, length of about 30% between wool and HoloFill II, then approximately the same difference can be expected for Miraflex. Second note: the Miraflex low frequency attenuation data was difficult to obtain due to line resonance effects thus there is some uncertainty associated with it. A similar problem but for the higher frequencies was present for the change in sound velocity in the stuffed line where the msec delay accuracy was also compromised by the line reflections and resonance. However in my opinion this data is very welcome as it extends the limits of Bradbury's fiber data which was stopped at about 50 Hz. (2) Data is extracted from L.de Martin Miraflex 6/13/98 termination study (C). Since it was necessary to reformat the data to conform the data to Bradury's fiber plot format, any errors are completely my responsibility

[ Back to the Transmission Line Speaker Page | The TLB | Appendix TOC ]