Baffle Diffraction Step30-april-12
[ OT Articles | Intro BDS | BaffleStep | BaffleStep Compensation | PLLXO | Sallen-Key | XO Design | DiAural ] |
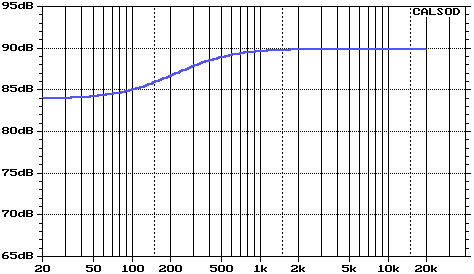
| An important loudspeaker design consideration is the baffle diffraction step, which is a result of the transition in the acoustical load presented to the loudspeaker. At high frequencies, a loudspeaker tends to project sound only in the forward direction that is, it has a 2 pi hemispherical radiation. At low frequencies, a loudspeaker undergoes a transition by which it begins to radiate sound in all directions, or a 4 pi spherical radiation. The result is an apparent reduction of bass response because the low frequency energy density is reduced in the forward direction where the listener is located. The overall effect is a gradual 6 dB shelving action at low frequencies, such that the bass is 6dB lower in level than the treble. See Figure 1 for a graph of baffle diffraction loss for an arbitrary 18" wide baffle. |
|
Figure 1. Effects of baffle diffraction for 18" wide baffle |
| Please note that this
diffraction loss curve is for an ideal loudspeaker mounted in a sphere, which exhibits
a very smooth transition. Other shapes, such as the common rectangular enclosure,
will introduce peaks and dips in the response, but the overall trend remains the
same. Very little may be done to predict these response anomalies as they are predominantly
spurious. The only reliable way to determine whether these peaks and dips are objectionable
is with listening tests and acoustic measurements. Baffle diffraction loss is a function of wavelength. The wavelength (l) of a given frequency at room temperature and standard atmospheric pressure may be found by the following equation: |
|
|
| The baffle diffraction step may be most accurately described as a loss of bass, and not a gain in treble. However, if we view a graph of baffle diffraction, the amplitude "rises" as we move from left to right across the frequency axis. As an approximation, the rise begins at the frequency whose wavelength is 8 times the smallest dimension of the baffle. This dimension is typically the width of the loudspeaker since most are tall and narrow. Using the same 18" baffle as in the previous example, the response would begin to rise at [1/8 * (13560/18)], or 94 Hz. Also, the maximum amplitude is attained at a frequency whose wavelength is twice the smallest dimension of the baffle; in this case [2(13560/18)], or 1.5 kHz. The -3dB point has been empirically determined to be: |
|
|
| The f3
for our arbitrary baffle width of 18" would be 253 Hz. All these calculations
are in agreement with the baffle diffraction loss simulation depicted in Figure 1.
Based on the above equation, it becomes clear that diffraction loss begins at higher
frequencies as the baffle width is decreased. Conversely, for an infinitely large
baffle, there will be no loss whatsoever as the loudspeaker is radiating into a 2
pi environment at all frequencies. This effect may be approximated by mounting the
loudspeaker within the plane of a large wall. The baffle diffraction step is generally viewed as a problem since it results in a non-flat frequency response. However, a mirror-imaged shelving network may be implemented to correct the frequency response to a flat amplitude. All that is needed is a network that attenuates high frequencies at a rate of 6 dB/octave, and "topping out" at 6 dB's of overall attenuation. Dr. John Murphy has documented an approach for compensating for the baffle step, so it will not be repeated here. I must say, however, that it is preferable to use an iterative process to develop a compensation circuit. This capability is offered by CALSOD and other such crossover optimization programs, after which the results should be verified with acoustic measurements. It is often possible to devise a compensation circuit that also incorporates filtering duties, rather than implementing a dedicated circuit. A dedicated circuit may introduce unnecessary series inductors into the circuit. These inductors are typically expensive, particularly if low DCR types are employed -- necessary to minimize performance degradation. Furthermore, inductor placement becomes more troublesome if mutual cross-coupling is to be avoided. However, those who do not possess sophisticated software/hardware will certainly find the dedicated circuit to be vastly superior to simply ignoring the phenomenon. Most (but not all) loudspeaker manufacturers publish response curves taken in a 2 pi environment. Therefore, the effects of baffle diffraction loss are not depicted. Consequently, if the frequency response curve indicates flat response, there will be a reduction in the bass response when the driver is placed in an enclosure and into a room, a 4 pi environment. This is a very important concept to understand since it will affect the crossover design and also the maximum sensitivity attainable with the particular driver. For example, suppose you have a woofer rated at 91dB/2.83V/1m and a tweeter also rated at 91dB/2.83V/1m. At first glance they would seem to be a perfect match for one another, at least in terms of sensitivity. However, baffle loss has not been factored in. In order to achieve flat amplitude response down to the low frequency limits of the driver, the midrange frequencies must be shelved down by 6dB, resulting in an 85dB sensitive woofer. This of course would also necessitate padding down the tweeter to mate with the woofer. In reality, it isn't necessary to shelve down the entire 6dB if a somewhat premature rolloff in the upper bass is acceptable, whereby allowing for a higher average sensitivity throughout the midband. This decision is a purely subjective design choice that should ultimately be based on the specific circumstances and the listener's preferences. Many commercially designed loudspeakers opt for this extra sensitivity and typically choose a 3-4dB shelf. Here again, an iterative optimization program is useful for determining a crossover network which will provide this response. No fancy ending to this story, but I do hope this information is somewhat helpful in explaining an esoteric and often misunderstood area of loudspeaker design. This information is an excerpt from an electrostatic loudspeaker paper I've written, and modified to cover a couple of issues not in the original copy. I know this overview is somewhat intimidating to a nontechnically-minded person, but I struggle for a way to simplify without also leaving out useful information. Good luck to all. |
|
[ Back to T-Line Speaker Page | OT Articles ] [ Intro BDS | BaffleStep | BaffleStep Compensation | PLLXO | Sallen-Key | XO Design | DiAural ]
|