|
Pearls from Martin
J. King Quarter Wave Design 11-december-05 The first time you visit http://www.quarter-wave.com/, you might get overwhelmed by the tremendous work done by Martin J. King. I have with great interest studied the information on the site, and Martin has been very patient answering my questions. When I realised quarter wave design was not that mysterious after all, I decided to write this article, which has been reviewed by Martin. Without the very helpful support from Martin, this article could not have been written. To fully understand the quarter
wave design, download MathCad and the MathCad worksheets. They are available for
private non-commercial use. *[a TL may also be used to create a highly non-resonant enclosure in which the goal is to completely eliminate the back wave of the speaker (ie a desirable goal if you are working with a midrange or a tweeter), and of course there is a continuous spectrum between these two] Problems with TL Resonance Systems
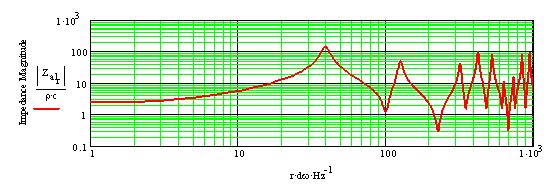
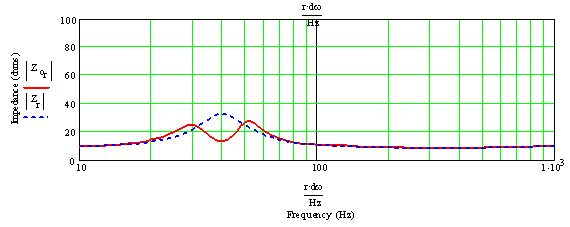
Figure 1: Transmission Line System and Infinite Baffle Impedance In this example, the driver resonance (Fs) is 40 Hz. This is shown by the blue line. The pipe is tuned to 40 Hz as well. Normally you would not set the pipe resonance equal to driver Fs. The red line is the combined system with the driver and cabinet, resulting in 2 new resonances. The first resonance (impedance peak) at 30 Hz is a combination of the air of mass in the pipe combining with the moving mass of the driver cone and voice coil oscillating on the driver's suspension. The second resonance peak about 53 Hz is the original cabinet resonance, but with the influence of the driver. At the original 40 Hz tuning frequency of the pipe, there is a dip, where the driver output is at the minimum and the opening output is at the maximum. This is not caused by resonance, but is the middle between the 2 new system resonances. MathCad is simulation tool — not a magic box -- With the MathCad worksheets, you are able to do what-if-analyses. This helps you to understand the consequences of changing the TL design. MathCad is not a guaranty your design will be a success; it can only predict accurate results from the input given. Use the alignment tables -- The best document to start with are Martin's Alignment Tables. This document includes very useful tables that allow you to quickly generate some baseline designs. It is a good starting point, even if you want to do further analysis using the MathCad worksheets. There are a few terms that need some explanation: Effective Length versus Physical Length -- At the opening, there is an acoustic impedance which makes the line behave as if it were slightly longer than the physical line at low frequencies. MathCad includes this impedance so depending on the geometry of your cabinet the actual tuning frequency might be a little lower than you would expect. Problems with baffle step response -- MathCad assumes the front baffle in you design is infinite, which it is not. Therefore the bass in your living room will be somewhat lower. It is the same thing you experience, if you move your speaker from the middle of your room and mount it on the wall, which will lift the bass. [Editor: Not familiar with Baffle Step? Baffle Diffraction Step -- An Introduction] Speed of sound in a stuffed line -- The TL resonates at one quarter of the wavelength of the frequency set as the tuning point. The wave length depends on the speed of sound. Damping of the pipe will slow down the speed of sound a little, and since the wave length depends on the speed of sound, a slight lowering of the tuning frequency will occur. However, this is not a dramatically reduction at all. A couple of Hz is what you will gain at the most. It is very difficult even to be able to measure if the tuning frequency has changed, as the impedance curve is damped and flat. Your local altitude and the temperature of the air has more of an impact on the tuning frequency than the stuffing.
The most important of the design parameters is the design of the cabinet: Length and geometry to set the tuning frequency -- Tuning frequency is set by the length of the line and the geometry. For a straight line, it is simply a quarter wave of the frequency. A tapered line (opening has a smaller area than the closed end of the pipe) is the smallest possible enclosure for the same frequency. A tapered line is very good at taming the unwanted upper harmonics. The output from the opening is broader and with slightly less output, compared to the straight line. An expanding line will be the longest line for the same tuning frequency. It has a high output level, unfortunately the frequency curve is very uneven. If you mass load the straight line, by making the area of the opening smaller than the cross section, the line will be shorter than the straight line for the same tuning frequency. A larger volume will, in general, increase the bass and also lower the tuning frequency a bit. Driver offset -- In a straight TL, moving the driver down approximately one third of the line will eliminate half the peaks in the higher harmonics. This is a very useful, old trick to tame the frequency response. The cost is slightly less bass. Stuffing to dampen nulls, ripples and impedance peaks -- The last option is stuffing, which should be relatively light so as not to attenuate the opening output too much. Stuffing will make the frequency curve smoother and dampen impedance peaks. The draw back is less bass. The balance between damping peaks and nulls, and still benefiting from the opening output is clearly seen in the MathCad worksheets.
Qts -- I use a Qts value of 0.35 to distinguish between high and low Qts. You might have another definition. Drivers with a high Qts perform better than driver with low Qts in a quarter wave design. On the other hand, the lower Qts driver seems to require less volume, thereby resulting in a smaller enclosure. Low Qts drivers have a roll off that starts earlier than high Qts drivers, and drivers with a moderate or high Qts will often result in the best low end performance. But this is also a matter of taste and preferences. "Good sound" is defined by you only. The output from the opening is broader with high Qts drivers, compared to low Qts drivers that have a narrower output from the opening. Drivers with a Qts lower than 0.30 seem to be difficult to control in a TL. Fs -- In a properly designed TL you can expect the bass to reach down half an octave — or maybe more - below the driver Fs. Vas -- In a TL, just like any other enclosure, Vas is a deterninant of the total enclosure volume. A good example of this can be seen by modeling an isobarik driver. The cross-section of the line halves just as the Va does (ie enclosure volume halves -- line length stays the same). Drivers with low Vas may require a box so small that at the required length the cross-section of the line is inadequet to create a good TL. It should be noted that a TL. in general, is fairly tolerant of differences in volume -- in this way similar to a sealed box with a Q below 0.707 (maximally flat/Butterworth)
A starting point could be to tune the enclosure 5-10 Hz above the driver's Fs if it is a low Qts driver. Tune the enclosure 5-10 Hz lower than the driver Fs, if the Qts is high. However, this is a guideline only. As you move the tuning frequency upwards, the output from the opening increases. And, not surprisingly, if you lower the tuning frequency you will at the same time also lower the output level from the opening. Set the cross section to 2-3 times Sd* at the closed end, and use a tapered geometry in the ratio 1:10. Or mass load the line by reducing the area of the opening, or use a port like in Martin's ML projects, to help control the higher harmonics. If your design allows it, set the driver down one fifth to one third of the line length -- play with the offset, sometimes small changes can be significant. By using MathCad, you will learn how to adjust the parameters and optimize your design. Every design will always will be a compromise of "competing" characteristics. *(Editor: Note that Martin uses sd as a convienient unit of area and is not really directly related to the cross-section of the line -- Vas is really the determining parameter) Using MathCad -- Download the free version of MathCad 8, from Martin's site, and the corresponding work sheets. The free version does not allow you to save the results. To save the information, all the plots can be saved by copy and paste. Other information about the driver properties and the enclosure geometry can be saved by doing a snapshot of the screen. I then use Paint to select the information to be saved. Remember, commercial use of Martin J. King's work is prohibited. Be sure your PC uses the dot as a decimal point. Otherwise, change the local setting to US. Read the user guide "Application Notes", as well as Martin's projects. These are templates for the worksheets, which are already filled in with data from the projects. Almost all the worksheets are derived from the Section worksheet. The other worksheets are adjusted for different enclosures to make input easier. Personally, I always use Sections work sheet, and a simulate as if it was a straight line, even if it is not. As long as the geometry does not change in the corner, this is no problem. Basic input -- Please
note Martin uses “d” instead of “s” in many abbreviations. Vad = Vas
etc. If you do not have the ability to do a measurement, and you do not know the T/S for the driver, try this site managed by Jan Fredriksson http://www.thielesmall.com/ Martin has a worksheet converting
from Vas to BL, or BL to Vas, since both Vas and BL are required
input. Driver parameters
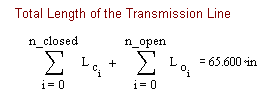
The n_closed = 0 means 1 section is used from the driver to the closed end, n_open = 2 means there are 3 sections from the driver to the open end. These are the number of sections MathCad will use to define the geometry, including the length of the pipe. If a tapered or expanding geometry is to be defined, more sections should be used to approximate the changing area as a function of the length.
Cross section area can be defined as a multiple of Driver Sd, so a pocket calculator is needed, or the actual dimensions or area can be input. By defining the length from driver to the closed end, you have defined the driver offset:
MathCad Results
Figure 2: Resulting Acoustic impedance for the Transmission Line This plot shows the resonance frequency for the cabinet alone. The tuning frequency is derived from the geometry defined above, but without stuffing, and is 40 Hz.
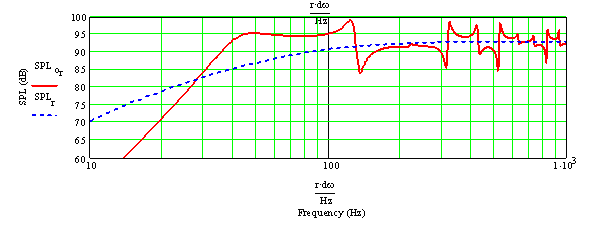
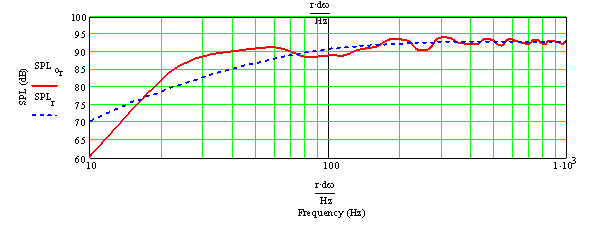
Figure 3: Far Field Transmission Line System and infinite Baffle Sound Pressure Level Response This plot shows the summed output from the driver and the opening. For comparison, the infinite baffle response is show as the blue line. Notice the first peak and drop. It is the 3rd harmonic (the fundamental 40 Hz times 3 = 120 Hz) where the standing waves generating the terminus output are 90 degrees out of phase with the driver output. By having the driver offset, this problem has already been reduced, and damping will reduce it even more. In your room the bass will be lower than shown on the plot, due to baffle step response, which might be somewhat compensated by room gain.
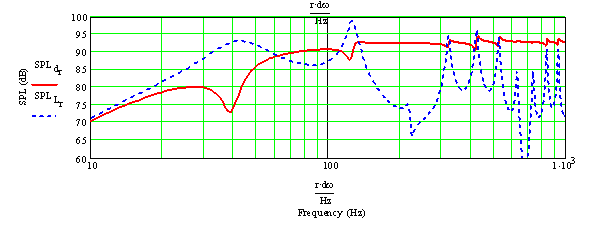
Figure 4: Woofer and Terminus Far Field Sound Pressure Level Responses The blue line is output from terminus alone; the red curve is the driver. This plot is very useful to see the effect of the damping and the driver offset.
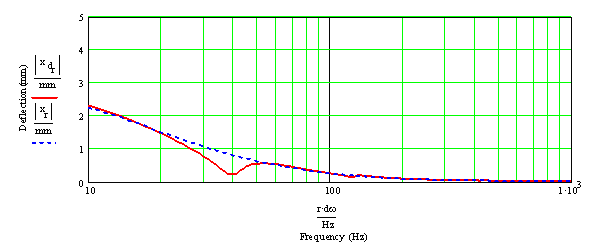
Figure 5: Woofer Displacement If you are familiar with bass reflex designs, you know a high pass filter is sometimes recommended to protect the driver below the tuning frequency. This is sometimes also the case in a TL. From the plots above, you can see there is a flat, high output down to 40 Hz. This might cause problems with uneven frequency response and unwanted resonances caused by the room gain. Furthermore, the low bass is missing.
Figure 6: Example of optimising the design Just by changing the length of the sections (not the opening), the tuning frequency is set to 23 Hz, which is lower than the driver Fs of 31 Hz. Now, there is a deeper bass and the roll-of looks more controlled. The stuffing is in the first half of the pipe only, with the same density as in the example above. This could be a nice sub, where
the cross over will eliminate the ripples above 100 Hz. Bjorn's website:http://www.kvart-bolge.com/
[ Back to T-Line Speaker Page | Design Info ]
|
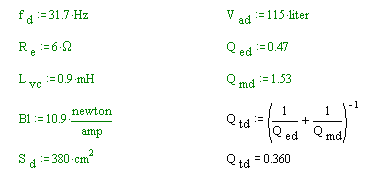



 .
.